Oscilátor s Wienovým můstkem

Úvod

Oscilátor s Wienovým můstkem je elektrický obvod generující sinusový signál. Stejně jako Phase-Shift  nebo Quadrature oscilátor si vystačí pouze s několika rezistory, kondenzátory a operačním zesilovačem.

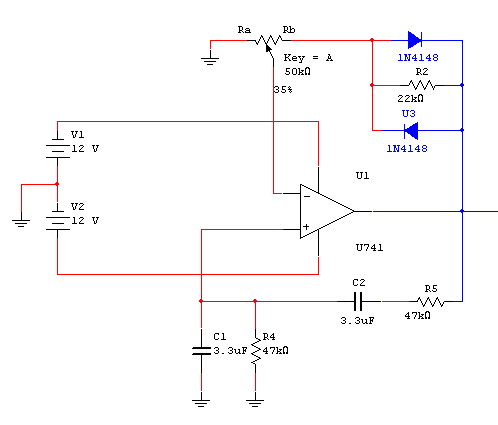Obrázek 1 - Oscilátor s Wienovým můstkem

Obrázek 2 - Phase-shift oscilátor

Obrázek 3 - Quadrature oscilátor

Odvození

Přenos Wienova můstku z obr. 1 mohu vyjádřit jako

$G(s)=\frac{\frac{R_4}{1+sC_1R_4}}{\frac{R_4}{1+sC_1R_4}+R_5+\frac{1}{sC_2}}$

Pro zjednodušení položím

$C=C_1=C_2$

$R=R_4=R_5$

Dostávám

$G(s) = \frac{sCR}{C^2R^2s^2+3CRs+1}$  

$G(jw) = \frac{jwCR}{1-C^2R^2\omega^2+3CRj\omega}$ 

Zjistím vlastní frekvenci systému

$1-C^2R^2\omega^2=0$

$w=\frac{1}{CR}$

Přenos se poté zjednoduší na

$G(jw) =\frac{1}{3}$

Nyní stačí rezistory \(R_a\) a \(R_b\) (trimmerem) nastavit zesílení operačního zesilovače na 3, čímž zajistíme výstup o konstantní amplitudě. Vzhledem k tomu, že elektronické součástky mají poměrně velké nejistoty, je do obvodu přidána kompenzace v podobě dvou diod a rezistoru, která dynamicky mění zesílení a udržuje jej na hodnotě 3. V případě poklesu pod tuto hodnotu by došlo k útlumu kmitání, naopak při vyšším zesílení by amplituda rostla.

Praktická realizace

Mým cílem bylo vytvořit generátor sinusového napětí o frekvenci 1 Hz a amplitudě 10 V, kterým bych nahradil generátor funkcí při práci s ultrazvukovým motorem.
Podle vzorce

$w=\frac{1}{CR}$

$f=\frac{1}{2\pi CR}$

jsem vypočítal potřebné hodnoty rezistorů a kondezátorů.

$R=47k\Omega$

$C=3.3\mu F$

V programu Multisim 9 Student Demo jsem simulací ověřil fungování oscilátoru s vypočtenými parametry a poté jsem generátor sestavil i z elektronických součástek. Narozdíl od simulace došlo v tomto případě, z nějakého důvodu, k desetinásobném zmenšení frekvence oproti očekávané hodnotě. Tento problém jsem jednoduše odstranil použitím rezistorů \(R=4.7k\Omega\). Domnívám se, že problém spočívá v použitých kondezátorech, které mohou dosahovat nejistoty -20%/+80% a jejichž kapacitu jsem neměl možnost změřit.

Obrázek 5 - výsledné zapojení generátoru sinusovky, řídicí elektroniky a ultrazvukového motoru

Simulinkové schéma

Obrázek 1 - Simulinkové schéma

Dalším z úkolů bylo zpracovat simulinkové schéma a ukázat na něm sledování rezonanční frekvence systému druhého řádu. K dispozici jsem měl téměř hotové, nicméně nefunkční, schéma vytvořené p. Hurákem.

Ve schématu na obr. 1 má blok popisující systém druhého řádu "na vstupu" proměnlivou vlastní frekvenci. V bloku Signal Builder jsou připraveny dva průběhy, jeden nechává frekvenci klesat lineárně a druhý exponenciálně. V obou případech je počáteční hodnota \(\omega_n \doteq 1.26\, . 10^5 \,rad.s^{-1}\; f=2\, . 10^4 \,Hz\), konečná hodnota je
\(\omega_n \doteq 1.01\, . 10^5 \,rad.s^{-1}\) \(f=1.6\, . 10^4 \,Hz\) , viz obr. 2.

Obrázek 2 - Připravené průběhy vlastní frekvence systému druhého řádu

V samotné zpětné vazbě je možné přepínat mezi analogovým oscilátorem řízeným napětí a PWM oscilátorem.

Obrázek 3 - Analogový oscilátor řízený napětím

Obrázek 4 - PWM oscilátor řízený napětím, střída 33%

Fázový detektor se skládá z jednoduchého násobení vstupních signálů a funkce signum. Násobením vzniká signál skládající se a) z harmonického signálu o frekvenci rovnající se součtu frekvencí násobených signálů a b) z harm. signálu s frekvencí rozdílu frekvencí násobených signálů. Matematicky to může být vyjádřeno následovně:

$2sin(\omega_it+\theta_i)cos(\omega_0t+\theta_0)= $

$=sin((\omega_i+\omega_0)t+\theta_i+\theta_0)+sin((\omega_i-\omega_0)t+\theta_i-\theta_0)$

Složku a) odfiltrujeme dolní propustí. Složka b) se po aplikování lineární aproximace zjednoduší:
Nechť $\theta_d=\theta_i-\theta_0$
$sin((\omega_i-\omega_0)t+\theta_d)\approx sin(\theta_d)\approx \theta_d$

Funkčnost tohoto schématu potvrzují frekvenční spektra na obrázcích 5 - 8. Na všech jsou vidět frekvence \(f=1.6\, . 10^4 \,Hz\) a \(f=2\, . 10^4 \,Hz\), tedy frekvence odpovídající vlastní frekvenci systému druhého řádu, viz. obr. 2.

Obrázek 5 - Frekvenční spektrum vstupního signálu, vlastní frekvence klesá exponenciálně

Obrázek 6 - Frekvenční spektrum výstupního signálu, vlastní frekvence klesá exponenciálně

Obrázek 7 - Frekvenční spektrum vstupního signálu, vlastní frekvence klesá lineárně

Obrázek 8 - Frekvenční spektrum výstupního signálu, vlastní frekvence klesá lineárně

Ultrazvukový motor PI M-661

Úvod

V pondělí 9.7. dorazil na katedru řídicí techniky balíček s lineárním ultrazvukovým motorem M-661 a řídicí elektronikou C184.161 od firmy PI.

Obrázek 1 - Ultrazvukový piezomotor PILine M-661

Obrázek 2 - Řídicí elektronika C184,  foto výrobce

Popis zapojení

Obrázek 3 - Řídicí elektronika po připájení pinů a připojení konektorů

Ke 3 pinům na levé straně řídicí elektroniky na obr. 3 je připojen řídicí signál. Tento signál je omezen na +/-10 V, polarita určuje směr pohybu piezomotoru. Spodní dva piny na pravé straně slouží k přivedení stejnosměrného napájecího napětí 12 V. Dráty ve žluté bužírce jsou výstupem řídicí elektroniky do samotného motoru, jsou připájeny k LEMO konektoru a přes něj k motoru. Poslední drát nahoře je uzemnění.

Pro úvodní rozběhnutí piezomotoru byla jako řídící signál použita sinusovka o frekvenci 1 Hz a amplitudě 10 V.

Obrázek 4 - Piezomotor v téměř krajní poloze vychýlení

V průběhu minulého týdne se motor nepodařilo rozpohybovat. Povedlo se jej pouze vychýlit do krajní polohy. Pro ukázku jak by měl tento motor vypadat v pohybu přikládám video.

Úvodní slovo

Tyto letní prázdniny jsem dostal možnost zúčastnit se letní stáže na katedře řídicí techniky v Oddělení pokročilých algoritmů pro řízení a komunikace (AA4CC) pod vedením Ing. Zdeňka Huráka, PhD. Na úvod bych chtěl p. Hurákovi poděkovat za možnost zúčastnit se této stáže a za jeho ochotu a přístup.

Téma mé letní stáže můžeme nejjednodušeji popsat těmito slovy - zpětnovazební sledování rezonanční frekvence ultrazvukového motoru. Než úkol popíšu přesněji, dovolím si v krátkosti vysvětlit, proč nějakou rezonanční frekvenci nějakých motorů vůbec sledovat.

Základem ultrazvukových motorů (ang. ultrasonic motors) je piezokeramika, která se vlivem střídavého vstupního napětí vhodně mechanicky deformuje a tuto deformaci převádí na pohyb. K tomuto deformování dochází s frekvencí, řádově, desítky až stovky kHz.

Existuje určitá frekvence, při které ultrazvukový motor pracuje nejefektivněji, dochází k nejlepšímu předání energie – rezonanční frekvence. Rezonanční frekvence se v čase mění, například vlivem zahřívání motoru. Pomocí zpětné vazby lze upravit vstupní signál tak, aby se těmto změnám přizpůsobil a rezonanční frekvenci sledoval.

Dosažení rezonanční frekvence se zjistí měřením fáze. Předpokládáme tlumený systém druhého řádu s koeficientem tlumení ζ<<0,707. Fázový posun mezi vstupním a výstupním signálem je v tomto případě při rezonanci –π/2.

Obrázek 1 - Bodeho frekvenční charakteristika systému druhého řádu pro různé hodnoty koeficientu tlumení

 
Ke sledování této fáze použijeme fázový závěs (ang. Phase-locked loop - PLL) . Fázový závěs se skládá z fázového detektoru, oscilátoru řízeného napětím a filtru dolní propust. Fázový detektor změří rozdíl fází mezi vstupním signálem a výstupním signálem z ultrazvukového motoru a vygeneruje signál úměrný fázovému rozdílu, který po průchodu dolní propustí vstupuje do oscilátoru, který generuje vstupní signál ultrazvukovému motoru.

Obrázek 2 - Systém druhého řádu ve fázovém závěsu

Vstupním signálem může být jak harmonický signál, tak pulsní signál. Vygenerovat pulsní signál je technicky jednodušší, než vytvořit signál harmonický, ale dochází ke zhoršení efektivity přenosu energie. Pánové Z. Hurák a P. Kujan vypracovali metodu zpětnovazebního sledování rezonance s použitím optimálního PWM (ang. Feedback tracking of resonance using optimal PWM switching), která nedostatky použití pulsního signálu ke sledování rezonance minimalizuje.

Mým úkolem bude praktická realizace problému obnášející zapojení potřebných přístrojů, instalaci software a zpracování měření.